算法设计笔记2024-9-19
19/9/2024
分析某个算法的三部曲:
- 是不是正确的(Is it correct?)
- 花了多长时间(How much time does it take, as a function of n?)
- 能不能更好(Can we do better?)
斐波那契算法(Fibonacci Algorithms)
经典的斐波那契数列:
0,1,1,3,5,8,13,21,34 |
传统算法: |
分析:

空间换时间算法: |
分析:
按照常理乍一看,应该是O(n),但是细细看:当n变大时,数字变大,计算加法等步骤就不再是常数了。
两个n位数字相加所需的时间大致与n成正比,所以大概与n^2成正比。
Big-O Notation(大O)
理论:Upper bounds上界,说直白点就是看最高的复杂度(就是增长的最快速的一项,可以更大

等于性:O(g(n))是一类函数的集合,但是为了方便写成f(n)=O(g(n)).
性质:
Reflexivity. f=O(f)
Constants: If f is O(g) and c > 0, then c f is O(g). [正常数倍的扩大缩小不会影响O]
Products: if f1 is O(g1) and f2 is O(g2) ,then f1f2 is O(g1g2) [乘法可以适用]
证明:
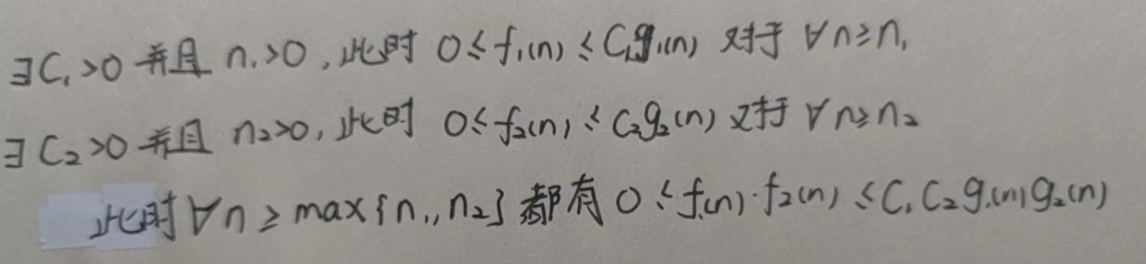
Sums: If f1 is O(g1) and f2 is O(g2) ,then f1+f2 is O*(max*{g1, g2}) [加法取最大]
Transitivity: If f is O(g) and g is O(h), then f is O(h). [O里能传递就完了]
Big Ω Notation(大Ω)
理论: Lower bounds下界,说直白点就是看最低的复杂度(就是增长的最低速的一项,可以更小
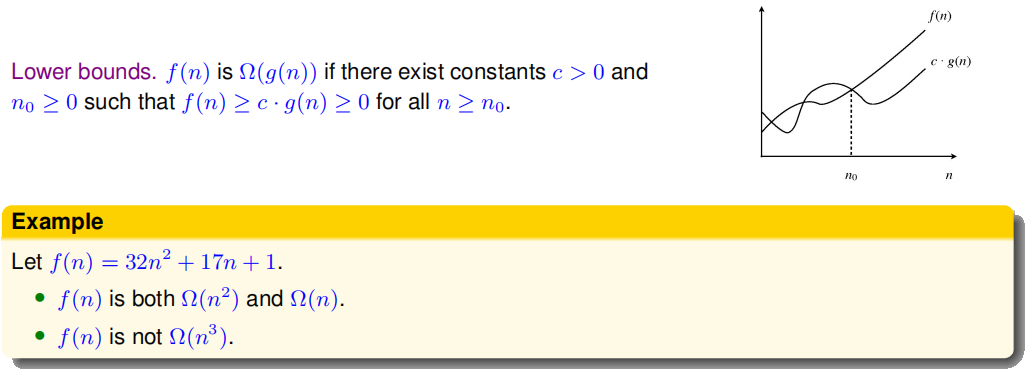
例题:
A:直接定义就能证明 B:sinx 和 cosx的反例
Big θ Notation(大θ)
理论: 就是最贴切的那一个
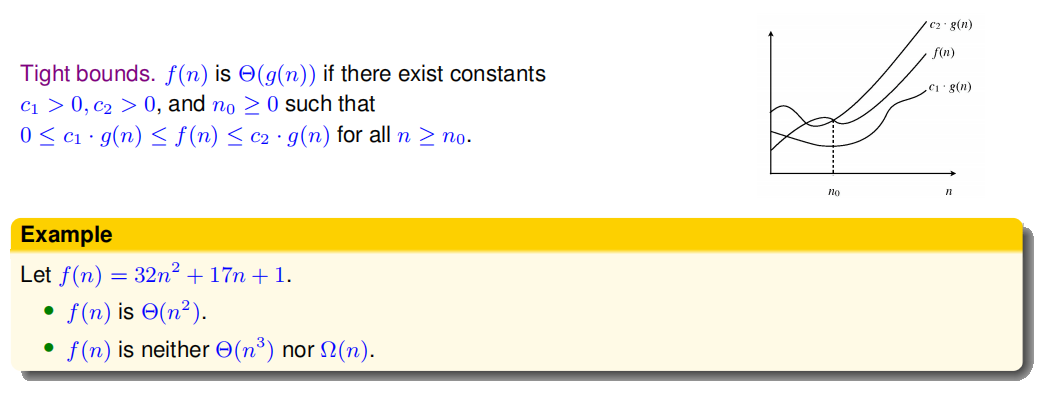
例题:

**A: **证明这种iff(当且仅当的意思),一定正的证一次,反的证一次,总结一句就完美
B: 
Ps: 
常用函数的渐进界(Asymptotic bounds for some common functions)
运用上面题目中的结论

第一个使用放缩夹逼定理,后两个用洛必达

本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 SEA WAVE!





