29/9/2024

书接上回，要想判断一个字符串是否符合某个token的定义，需要有限自动机。

有限自动机（Finite Automata）

有限自动机是一个五元组：一个字母表，一个有限的状态集合，一个初始状态，一组终结状态的集合（必须是S的子集）和transition（状态的变化）。

系统初始状态是s1在接受到a之后，变化到s2状态。输入如果是一串字符串就是一直重复刚刚类似的过程，直到最后进入了一个终结状态（accept state），代表这个输入被接受了，这个字符串属于这个自动机对应的regular language。

举个例子：只接受一串1之后跟了一个0的有限自动机

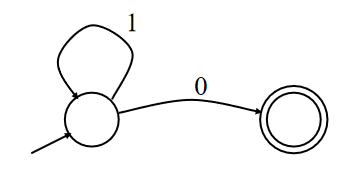
比如接收1110，而11101就会reject 0后的1

在举两个例子

​

左边这个是transition 不唯一了，右边这个是我们加上的E（一佩龙）转移，说明可以不接收字符就可以无条件从A转移到B。

后两个例子明显和第一个例子有区别，我们把transition是确定的叫做DFA（deterministic finite automata），把后面的不确定transition叫做NFA（nondeterministic finite automata）。但是两种都是非常简单的计算模型，我们在实现的时候，只需要当前状态和input就可以决定我们的动作，和之前无关，同时状态的数量也是有限的。

只要有一种能够到达终结状态就行。得出结论就是：NFA和DFA能够识别的东西是相同的。DFA写出来的代码是很容易的，只需要n * n的一张transition表就可以了。但是有个缺点直接构造DFA会比较困难，更加麻烦（ 同一个NFA变成DFA的时候，有可能其状态会指数增长），所以我们要先用regular expression 构造NFA。

用描述token的正则表达式来构造NFA

下边我们来看一下，我们用regular expression来描述词法，描述好词法以后，我们希望用这个regular expression来构造出NFA，再转化成DFA，然后就变成一个查表判定的过程。整体流程如下图，我们现在做的就是箭头的地方

这个步骤的5个构造法则：

​

举个例子： 就是把上面的公式套进去

NFA->DFA

五个小策略：
  1. 模拟NFA
  2. 每个DFA的状态都是非空NFA状态的子集
  3. DFA的起始状态是：所有E（一佩龙）能够到达的状态，都是DFA的起始状态
  4. 从一个状态S接收一个字符a到另一个状态S’，我们要看看碰到每个字母表中的字符会变到哪里去，从而增加状态转移。、
  5. DFA的终止状态就是NFA的终止状态

举个例子： 这个步骤执行可以，但是可能出现指数爆炸

用查表描述一个DFA

这个表里，横轴是字符集合，纵轴是状态集合。

有了这个表，就可以从start_state开始一个个字符走，如果到了终止状态，就是符合的可接受的；如果到一半走不下去，就说明reject了。T[i,a] = k表示状态Si接受到了a到了状态Sk。

我们有一些自动化的工具，一般叫做lex，比如flex和jlex。也就是我们写regular expression，它会生成NFA, DFA，DFA的表，然后我们就可以进行查表判定。

压缩DFA的状态数目

NFA变DFA的状态会有很多，我们希望对DFA的状态进行简化一下，压缩一下状态。比如说我们有上面的这个DFA，有7个状态ABCDEF。要做化简实际上是做一个等价类，也就是说当我们状态S1能够接收字符串s的时候，S2也能接收s，方法如下：

这上面起始就走完完了最上面的那张图里的步骤

因为我们的词法分析不是回答yes/no的事情，我们要切割出来某个子token串，来判断其是否属于L（Ri）还要满足maximal munch和priority rule。已经落到某一类的时候，我们需要继续往前走来找到更长的符合条件的情况。所以刚才那个table我们只是有了一个基础的这个东西，我们要把这个东西扩展，扩展成我们的词法可以用的这个东西

把DFA扩展使其支持那两个原则

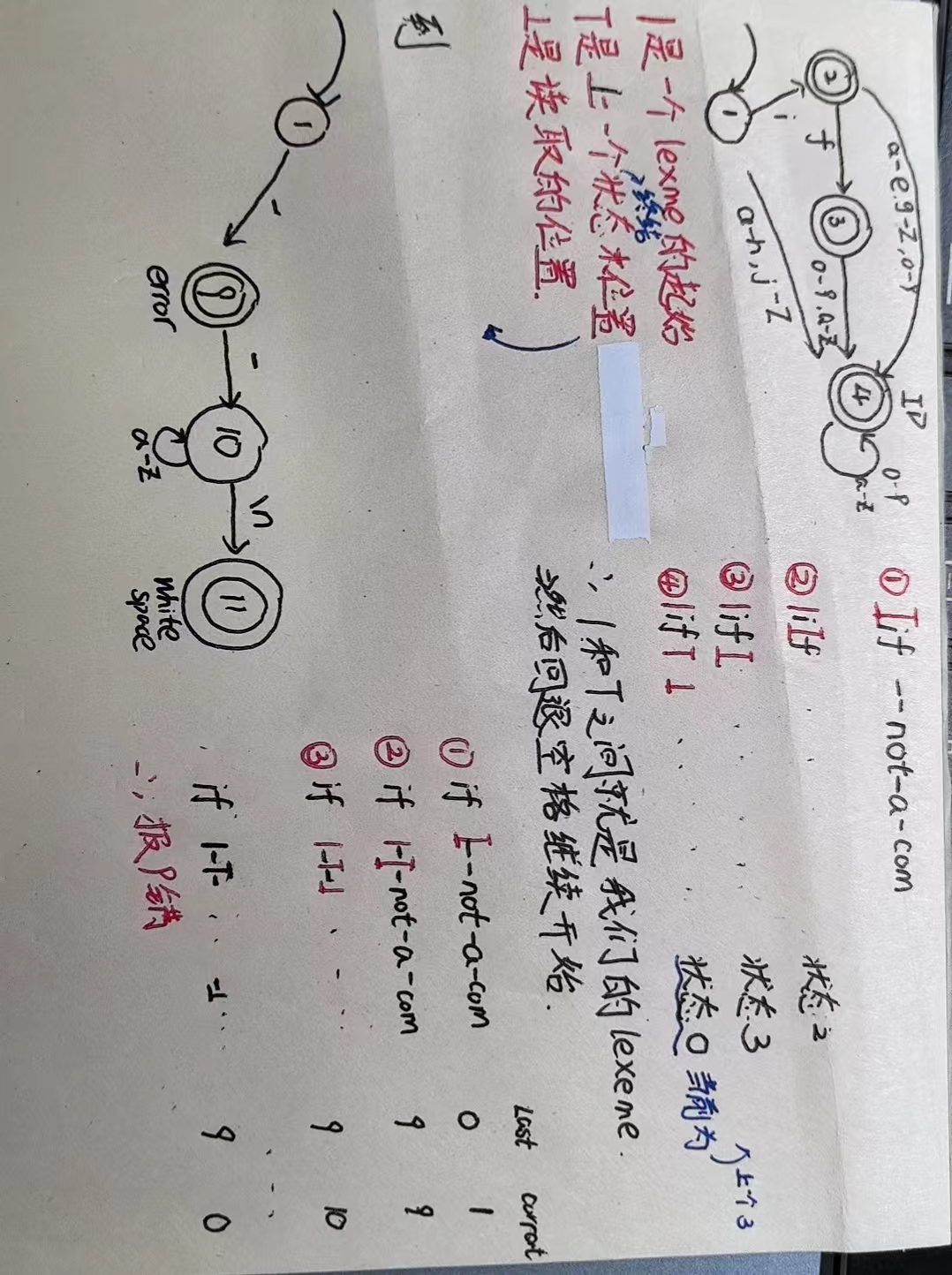
举个例子：前面是我们规定的一个词法：分别keyword(if), identifier(返回ID), number, 实数，注解（两个”–”+一串字母+\n，或者space, \n, tab），错误（如果前面的都不能匹配，就报错了）

现在我们输入：if –not-a-com

流程是这样子的：

我们需要增加一些状态。

》》》

为了满足优先级原则：

显然abb是a*b+的子集，但是abb优先，同时进入4和6作为accept states的时候，应该是4优先，因为4的优先级高。我们把NFA画成DFA。

LEX工具

我们写代码的时候还是写一串declearation，我们还需要写一串花括号。报错的时候我们要往前走。我们不但要有识别，我们还要做一些动作。花括号里的东西都是C程序。

我们写一些declearation（regular expression）和action（C），有一个简单的编译器生成C代码。生成了C以后，就可以放到编译器里头，编译出可执行的文件。a.out就是输入一个tiger program，通过a.out运行以后能就变成了一个token串。

LEX有三部分：

  • %{ … %}：C代码。
    • tokens.h会定义一些token的类型
    • union yylval ：因为每个token对应一个lexeme， 所以一个lexeme 可以用一个整数int来表示
    • string sval ：就是关键词，用字符串表示就行
    • double fval：实数用double类型表示
    • int charPos： 表示当前character的位置，开始都是1，每一次可以调整
    • length()当前匹配了多长，char_pos_每次的起始位置
  • lex definition：定义一些宏，比如用digits替换掉[0-9]+
  • %%开始：regular expression + action
    • if 直接往前走
    • identity，除了往前走外，还要把lexeme算出来，yytext就是|和T之间的字符串；其他的同理。

处理嵌套注释

它在lex里头是可以支持的，这个支持就是说我们会有两个start_state。一个叫inital，一个comment，在lex definition声明了两个初始状态。正常情况下都是initial的if，字符串。如果我们碰到了(* 就说明我们进入了一个可能comments的情况，也就是我们进入了一个新的start_state（COMMENT），在这个状态下碰到任意输入都无所谓，直接过滤掉。过滤掉以后，一直到 *)，它要回到INITIAL的情况。一开始我们想让它进入INITIAL状态，我们就用最后一行。也就是BEGIN INITIAL；吃掉的一个字符要还回去，也就是yyless(1)。